
👉পর্ব : ১
✍ বিষয় : লিনিয়ার রিগ্রেশন কি ?
পরিচিতি
পরিসংখ্যানগত মডেলিং এ, রিগ্রেশন রিগ্রেশন (অথবা প্রত্যাগতি বিশ্লেষণ, ইংরেজি: Regression Analysis) হচ্ছে কতগুলো পরিসংখ্যানগত প্রক্রিয়ার সেট যার মাধ্যমে চলকসমূহের মধ্যে বিদ্যমান সম্পর্ক নির্ণয় করা হয় । কতগুলো চলকের মডেলিং ও বিশ্লেষণের জন্য এতে অনেকগুলো কৌশল অন্তর্ভুক্ত রয়েছে, যেখানে মূল লক্ষ্য হচ্ছে একটি অধীন চলকের সাথে এক বা একাধিক স্বাধীন চলক (বা 'সূচক') এর মধ্যকার সম্পর্কের নির্ণয়। আরও সুনির্দিষ্টভাবে বললে, যে কোন একটি স্বাধীন চলকের মান পরিবর্তন করলে এবং অন্যান্য স্বাধীন চলকসমূহকে স্থির রাখলে, সাধারণত কীভাবে অধীন চলকটির (বা 'নির্ণায়ক চলক') মানের পরিবর্তন হয়, রিগ্রেশন বিশ্লেষণ তা বুঝতে সাহায্য করে।
লিনিয়ার রিগ্রেশনের এপ্লিকেশন
লিনিয়ার রিগ্রেশন মডেলগুলির বাস্তব জগতে অনেক প্রয়োগ রয়েছে যেমন অর্থনীতি (উদাঃ মূল্য বৃদ্ধির পূর্বাভাস), ব্যবসায় (উদাঃ পণ্য বিক্রয়, কর্মচারীর কার্যকারিতা সম্পর্কে ভবিষ্যদ্বাণী করা), রাষ্ট্রীয় বিজ্ঞান (উদাঃ ধর্ম , বর্ণ , লিঙ্গ বা জাতি থেকে রাজনৈতিক জনপ্রিয়তার পূর্বাভাস), স্বাস্থ্যসেবা (উদাঃ ওজন থেকে রক্তচাপের মাত্রা, জৈবিক কারণ থেকে রোগের সূচনা) এবং আরও অনেক কিছু সম্পর্কে ভবিষ্যদ্বাণী করা যায় |
লিনিয়ার রিগ্রেশনের ধারণা
লিনিয়ার রিগ্রেশন মডেলগুলির বাস্তব জগতে অনেক প্রয়োগ রয়েছে যেমন অর্থনীতি (উদাঃ মূল্য বৃদ্ধির পূর্বাভাস), ব্যবসায় (উদাঃ পণ্য বিক্রয়, কর্মচারীর কার্যকারিতা সম্পর্কে ভবিষ্যদ্বাণী করা), রাষ্ট্রীয় বিজ্ঞান (উদাঃ ধর্ম , বর্ণ , লিঙ্গ বা জাতি থেকে রাজনৈতিক জনপ্রিয়তার পূর্বাভাস), স্বাস্থ্যসেবা (উদাঃ ওজন থেকে রক্তচাপের মাত্রা, জৈবিক কারণ থেকে রোগের সূচনা) এবং আরও অনেক কিছু সম্পর্কে ভবিষ্যদ্বাণী করা যায় |
মূল ধারণাটি হল আমরা যদি পর্যবেক্ষণ করা তথ্যের সাথে লিনিয়ার রিগ্রেশন মডেলটি ফিট করতে পারি তবে আমরা ভবিষ্যতের মানগুলি পূর্বাভাস দেওয়ার জন্য মডেলটি ব্যবহার করতে পারি। উদাহরণস্বরূপ, ধরে নেওয়া যাক আমরা হিস্টরিকাল তথ্য থেকে খুঁজে পেয়েছি যে কোনও বাড়ির দাম (P) তার আয়তন-আকার (S) এর উপর রৈখিকভাবে নির্ভরশীল ।
আসলে আমরা দেখতে পেয়েছি যে কোনও বাড়ির দাম তার আকারের 90 গুণ বেশি। সমীকরণটি দেখতে হবে:
P = 90*S
এই মডেলটির সাহায্যে আমরা তখন কোনও বাড়ির দাম অনুমান করতে পারি। আমাদের যদি একটি বাড়ি থাকে যা 1,500 বর্গফুট হয়, আমরা এর দামটি গণনা করতে পারি:
P = 90 * 1500 = 135,000
এই পোস্টে, আমরা কভার করবো :
- লিনিয়ার রিগ্রেশনের এর মৌলিক ধারণা এবং গাণিতিক ব্যাখ্যা
- সাইকিট-লার্ন ব্যবহার করে কিভাবে লিনিয়ার রিগ্রেশন এর প্রয়োগ করা যায়
মূল ধারণা এবং গণিত
লিনিয়ার রিগ্রেশন মডেলটিতে দুটি ধরণের ভেরিয়েবল রয়েছে:
- ইনপুট বা প্রেডিকটর ভেরিয়েবল হলো এমন একটি ভেরিয়েবল (গুলি) যা আউটপুট ভেরিয়েবলের মান অনুমান করতে সহায়তা করে। এটি সাধারণত X হিসাবে উল্লেখ করা হয়।
- আউটপুট ভেরিয়েবল এমন একটি ভেরিয়েবল যা আমরা প্রেডিক্ট করতে চাই। এটিকে সাধারণত Y হিসাবে উল্লেখ করা হয়
লিনিয়ার রিগ্রেশন ব্যবহার করে Y অনুমান করতে আমরা সমীকরণটি ধরে নিই:
Yₑ = α + β X
যেখানে Yₑ হ'ল আমাদের লিনিয়ার সমীকরণের উপর ভিত্তি করে Y এর এস্টিমেটেড বা প্রেডিক্টেড মান।
আমাদের লক্ষ্য হলো পরিসংখ্যানগতভাবে α এবং β প্যারামিটারের অর্থপূর্ণ মান বাহির করা যা, Y এবং Yₑ এর মধ্যে পার্থক্য হ্রাস করে |
আমরা যদি এই দুটি প্যারামিটারের সর্বোত্তম মানগুলি নির্ধারণ করতে সক্ষম হয়ে থাকি, তবে X এর মান বিবেচনা করে Y মানগুলির গণনা করার জন্য আমাদের বেস্ট ফিটের লাইন বা X এবং Y যা এর মাঝে লিনিয়ার রিলেশন খুঁজে পাবো |
সুতরাং, আমরা কীভাবে α এবং β অনুমান করব? আমরা ordinary least squares. নামে একটি পদ্ধতি ব্যবহার করতে পারি।

সবুজ রেখাগুলি প্রকৃত মান Y এবং প্রেডিক্টেড মান Yₑ মধ্যে পার্থক্য নির্দেশ করে
Least-squares পদ্ধতির উদ্দেশ্য হলো α এবং β এর এমন কিছু মান বাহির করা, যা হ্রাস করে Y এবং Yₑ এর মধ্যে বর্গক্ষেত্রের বিয়োগফলের যোগফল | আমরা এখানে derivation মধ্য দিয়ে যাব না, তবে ক্যালকুলাস ব্যবহার করে আমরা দেখাতে পারি যে অজানা প্যারামিটারগুলির(α এবং β) মান নিম্নরূপ:
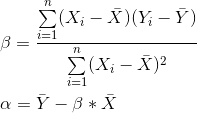
যেখানে
- X̄ হলো X মানগুলির গড়
- Ȳ হলো Y মানগুলির গড়।
লিনিয়ার রিগ্রেশনের গাণিতিক ব্যাখ্যা বিস্তারিত জানতে এই ভিডিও টি দেখুন
Linear Regression From Scratch
দুটি পাইথন মডিউল ব্যবহার করে খুব সহজে আমরা লিনিয়ার রিগ্রেশন পরিমাপ করতে পারি যেমন :
- scikit-learn — a module that provides simple and efficient tools for data mining and data analysis.
- statsmodels — a module that provides classes and functions for the estimation of many different statistical models, as well as for conducting statistical tests, and statistical data exploration.
