👉Part : 01

✍ Topic : Intuition Behind Principal Components Analysis(PCA)

পরিচিতি

Principal component analysis(PCA) বহুল ব্যবহিত Dimensionality Reduction Algorithm। PCA মুলত একটি ডাটাসেটে ডাটাগুলোর লম্ব অভিক্ষেপ( Orthogonal Projection ) খুজে বের করে। Orthogonal projection এর মাধ্যমে PCA ডাটাসেটের সর্বোচ্চ ভ্যারিয়েন্স বা Variance (পরিসংখ্যানে ভ্যারিয়েন্স একটি ডেটা সেটের সংখ্যার মধ্যে ব্যাপ্তি পরিমাপ করে ) খুজে বের করে এবং এর সাহায্যে ডাটাসেট এবং ফিচার (Feature) মধ্যে লিনিয়ার কোরিলেশন (linear-correlation ) বের করা যায়। অর্থাৎ , আমাদের কাছে যদি একটি নিদিষ্ট ডাটাসেটের লিনেয়ারলি কররেলেটেড(linearly correlated ) কিছু ফিচার থাকে, তাইলে PCA এর মাধ্যমে orthogonal direction খুজে বের করতে পারবো যা আমদের ডাটাসেটের এর সমস্ত ডাটাকে একটি direction এ তুলে ধরতে পারে ।

PCA কতগুলি principal component নিয়ে গঠিত, চলুন Principal component কি দেখে নেয় ।

Principal component

Principal component হলো প্রাথমিক ভ্যারিয়েবল থেকে সৃষ্ট Linear combination or mixure এর মাধ্যমে তৈরী একটি নতুন ভ্যারিয়েবল । নতুন ভ্যারিয়েবল টি কতগুল Principal component নিয়ে গতিত। Principal component এক বা একাধিক হতে পারে। অর্থাৎ, একটি ডাটাসেটের ডাইমেনশন যদি ১০০ হয় তবে তার principal component হবে ১০০টি । Principal components ডাটার অধঃক্রম তথ্য এর উপরে ভিত্তি করে নিম্নোক্ত বিন্যাস আকারে সাজানো থাকে ।

principal components = 1st principal, 2nd principal, 3rd principal, 4th principal ................nth principal.

নতুন ভ্যারিয়েবল টি সম্পূর্ণভাবে আনক্ররেলেটেড( uncorrelated ) হয়ে থাকে এবং প্রাথমিক ভ্যারিয়েবল এর অধিকাংশ ইনফরমেশন সঙ্কুচিত হয়ে 1st principal component তৈরী করে থাকে । PCA চেষ্টা করে অধিকাংশ তথ্য বা ভ্যারিয়েন্স 1st principal component এ রাখার তারপর অবশিষ্ট অধিকাংশ তথ্য বা ভ্যারিয়েন্স 2nd principal component এ রাখার এবং এইভাবে তথ্য বা ভ্যারিয়েন্স এর উপরে ভিত্তি করে principal components এর বিন্যাস তৈরী হয়ে থাকে। নিম্নে ছিত্রে দেখানো হলো।

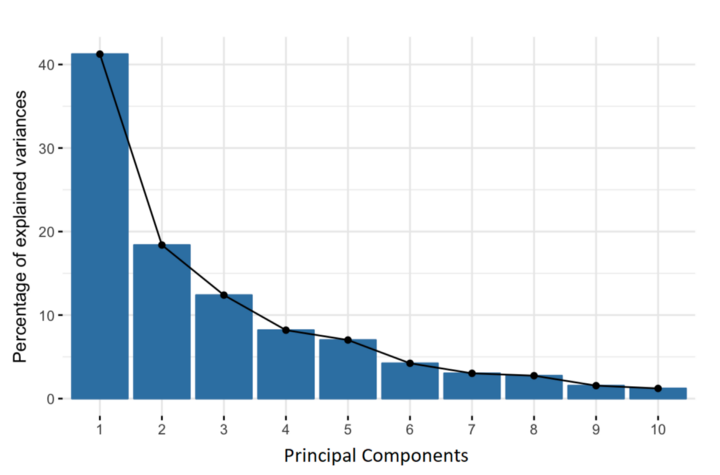
উপরিউক্ত বিন্যাস (higher information to lower information) আকারে principal components গুলা সাজিয়ে খুব সহজে আমরা কম তথ্য হারিয়ে একটি Lower dimensional Dataset( new Dataset) তৈরী করতে পারি ।

সুতরাং, এইভাবে lower information principal component বাদ দিয়ে অবশিস্ট principal component নিয়ে প্রাথমিক ভ্যারিয়েবল (Raw Dataset) থেকে নতুন ভ্যারিয়েবল( new Dataset) তৈরী হয়ে থাকে ।

উদাহরণ

আমরা জানি একটা ডাটাসেট এর ডাইমেনশন যদি 100D হয় তবে তার principal component ও হবে ১০০টি. PCA যখন dimension reduction করে তখন লো(low ) ভ্যারিয়েন্স ফিচার কে বাদ দিয়ে হায়ার(higher ) ডাইমেনশন থেকে লোয়ার(lower ) ডাইমেনশন ডাটাসেট তৈরী করে থাকে . অর্থাৎ optimal principal component খুঁজে বের করার জন্য PCA সব সময় low information feature or low variance data কে noise হিসাবে বিবেচনা করে . এই noise feature গুলা বাদ দিয়ে PCA একটা নতুন ডাটাসেট তৈরী করার থাকে যার ডাইমেনশন হয় মূল ডাটাসেট এর ডাইমেনশন থেকে অনেক কম ( Depdnd on infomation gather by each princiapl component).

ধরেন মূল ডাটাসেটের নাম A এবং এর ডাইমেনশন হচ্ছে 100D . অর্থাৎ A ডাটাসের principal component ও হবে ১০০টি . ১০০টি principal component এর মাঝে প্রথম থেকে ২০টি principal component e ৯৬% ডাটার তথ্য বা ভ্যারিয়েন্স ধরিয়া রাখে .

PCA তখন ২১ - ১০০ পর্যন্ত ডিমেনশনের ডাটাকে noise হিসাবে বিবেচনা করে ওগুলা রিমুভ করে দিবে, বাকি ২০ principle component নিয়ে একটি নতুন ডাটাসেট তৈরী করবে. নতুন ডাটাসেট টির নাম হলো B.

সুতরাং, PCA প্রয়োগ করে তৈরী B ডাটাসেট টি A ডাটাসেটের ৯৬% information তথ্য বা ভ্যারিয়েন্স ধরিয়া রাখে এবং higher dimensional dataset (A: 100 dimension) থেকে lower dimensional dataset( B : 20 dimension) তৈরী হয়